Nouvelle Structure Arithmétique et Géométrique des Nombres Premiers

Vers un algorithme prédictif et parallélisable de génération des nombres premiers

Préambule

L’étude des nombres premiers est au cœur des mathématiques depuis l’Antiquité. Leur répartition apparemment chaotique cache une structure d’une extraordinaire complexité.

La recherche des nombres premiers repose historiquement sur des méthodes de test successif, toutes dérivées plus ou moins du crible d'Ératosthène. Pour affiner la connaissance de ces nombres, la théorie des nombres s'est attelée à en déterminer le taux de croissance. À la fin du XVIII^e siècle, Gauss et Legendre ont conjecturé que cette quantité était « proche de » \( \frac{x}{\ln(x)} \), où \( \ln \) est la fonction logarithme népérien.

Cette affirmation constitue le théorème des nombres premiers, prouvé indépendamment par Hadamard et La Vallée Poussin en 1896, grâce à l’étude de la fonction zêta de Riemann, définie pour \( \text{Re}(s) > 1 \) par :

\[ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} = \prod_{p\ \text{premier}} \left(1 - \frac{1}{p^s}\right)^{-1} \]

L'hypothèse de Riemann stipule que tous les zéros non triviaux de \( \zeta(s) \) ont une partie réelle égale à \( \frac{1}{2} \). Elle équivaut à une majoration beaucoup plus serrée de l'erreur dans l'approximation de \( \pi(x) \), donc à une distribution plus régulière des nombres premiers :

\[ \pi(x) = \text{li}(x) + O\left( \sqrt{x} \ln(x) \right) \]

Il est donc naturel de s'interroger sur la relation structurelle entre la fonction de comptage \( \pi(x) \) et les zéros non triviaux de \( \zeta(s) \), dans le cadre d'une méthode algorithmique de génération des nombres premiers.

Notre approche repose sur une structure arithmétique et géométrique, permettant de cibler directement les entiers de forme \(6k \pm 1\) dans des intervalles ordonnés. En associant cette méthode à une estimation préalable de \( \pi(x) \), il devient possible de :

Découper efficacement l'espace de recherche pour répartir dynamiquement les tâches entre plusieurs unités de traitement indépendantes (petits modules exécutés en parallèle).
Explorer exhaustivement chaque intervalle jusqu'au dernier, garantissant l'ordre naturel des 100 premiers générés.
Contrôler, en fin de traitement, la continuité entre les sous-intervalles \(i\) et \(i+1\) pour éviter doublons ou ruptures.

Remarque : dans certains langages de programmation, ces unités parallèles peuvent prendre la forme de fibres — structures légères permettant d'exécuter plusieurs tâches simultanément sans surcharge, plus souples que les processus classiques ou les threads.

Ce mécanisme se veut à la fois conforme aux lois analytiques classiques issues de \( \zeta(s) \), et compatible avec une implémentation algorithmique moderne.

À propos de la taille en bits : plus le nombre de bits est élevé, plus le nombre aléatoire initial est grand. Cela permet de cibler des nombres premiers de grande taille, utiles dans des domaines comme la cryptographie. Une taille de 12 bits donnera des nombres modestes ; 2048 bits permet d'atteindre des entiers immenses.

Un module interactif est proposé ci-dessous : il permet à l’utilisateur de saisir un nombre aléatoire (de 12 à 2048 bits) via un formulaire, et d’obtenir en retour la liste des 100 nombres premiers consécutifs à partir de ce point. Cette liste pourra être téléchargée au format JSON pour analyse externe.

1. La structure arithmétique proposée

Elle repose sur la formule de base suivante :

\[ N = pn + \frac{p(p+1)}{2} = p\left(n + \frac{p+1}{2}\right) = p \cdot q \]

où \( p,\ n\ \text{et}\ q = n + \frac{p+1}{2} \) sont des entiers naturels. Cette construction définit une table virtuelle dans laquelle chaque entier impair peut être positionné selon une organisation factorielle régulière.

2. Localisation des nombres premiers par les carrés impairs

Les carrés de la forme \( (9 + 6t)^2 = \left(3(3 + 2t)\right)^2 \) sont repérables sur deux colonnes :

Une colonne paire : \(p = 2(3 + 2t)\)
Une colonne racine carrée : \(p = \sqrt{N}\)

Entre le carré de type \( (9 + 6t)^2 \) et son suivant \( (9 + 6(t+1)^2 \)

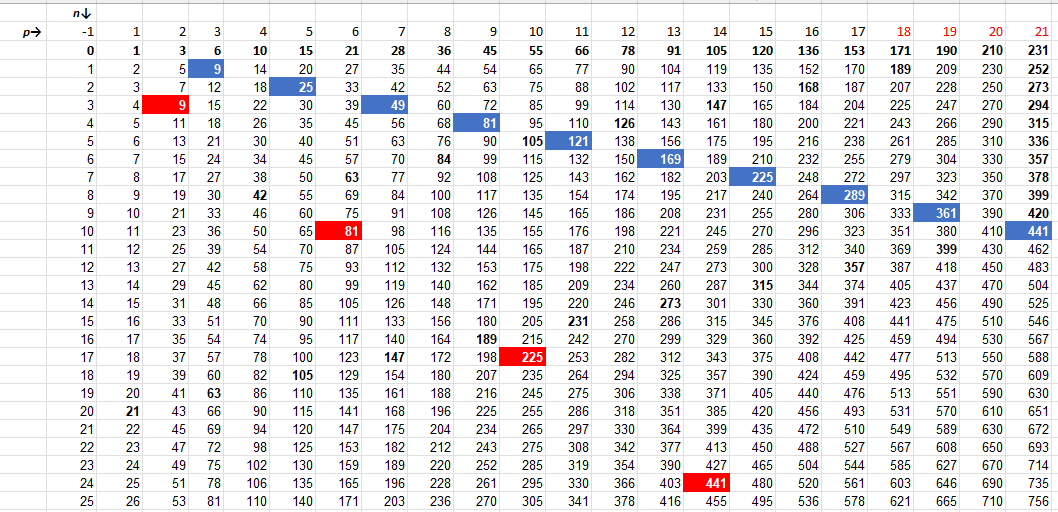
Les propriétés de divisibilité des colonnes \(p = 2k(3 + 2t)\) permettent de renforcer le filtrage arithmétique :

Si \(k\) est divisible par 3, alors l'expression est divisible par 6, quelle que soit la valeur de \(t\);
Si \(3 + 2t\) est divisible par 3, alors l'expression est divisible par 6, quelle que soit la valeur de \(k\);
Si ni \(k\) ni \(3 + 2t\) ne sont divisibles par 3, alors l'expression n'est pas divisible par 6.

3. Localisation des nombres premiers par les racines triangulaires

3.1 Notion de racine triangulaire

Un nombre triangulaire est défini par la relation : \[ T = \frac{k(k+1)}{2} \]

La racine triangulaire d’un entier \( T \) est le \( k \) tel que : \[ k = \frac{-1 + \sqrt{1 + 8T}}{2} \]

Cette racine est entière uniquement si \( T \) est triangulaire. Cette propriété ouvre une piste structurante pour la localisation des premiers dans la structure proposée.

3.2 Organisation en groupes et classes

La formule de base \[ N = pn + \frac{p(p+1)}{2} = p\left(n + \frac{p+1}{2}\right) = p \cdot q \] montre que pour n = 0 nous pouvons identifier tous les nombres triangulaires de 3 à l'infini.

Les nombres triangulaires peuvent être répartis en classes :

Classe \( C_{11} \) : \( 3, 15, 36, 66, \ldots \)
Classe \( C_{12} \) : \( 6, 21, 45, 78, \ldots \)
Classe \( C_{13} \) : \( 10, 28, 55, 91, \ldots \)

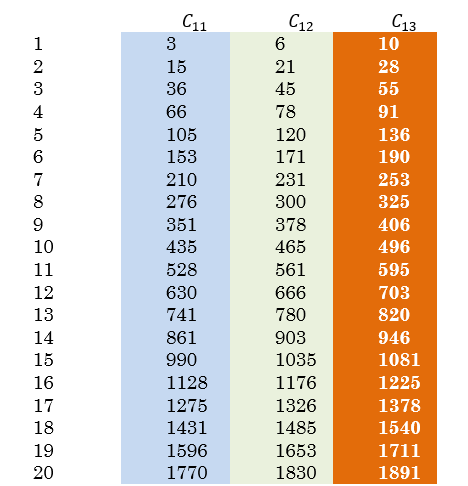
Les deux premières classes \( C_{11} \) et \( C_{12} \) sont systématiquement divisibles par 3. La troisième classe \( C_{13} \) présente une propriété remarquable : les racines triangulaires des éléments de \( C_{13} \) correspondent à des nombres premiers dans de nombreux cas.

3.3 Fonction générative des nombres premiers

À partir de l’observation précédente, une fonction de génération des nombres premiers peut être construite selon :

\[ \text{Si } x \text{ est pair : } s = 3x - 1 \quad \text{; si } x \text{ est impair : } s = 3x - 2 \]

La fonction suivante permet d'extraire tous les nombres premiers, dans l'ordre croissant de leur apparition dans n'importe quel intervalle de nombres entiers

  public function testProduitPremier(){ 
    $start_time = microtime(true);// nécessaire pour calculer le temps de début de l'exécution
    $tab = [];
    $bits = 2048; // Fixe le nombre de bits des nombres premiers désirés. Peut aller jusqu'à 4096 et même au-delè
    $x = $this->renvoieNombreDecimalAvecEnviron($bits);
    $classe = 1; // pour gmp_prob_prime.Mettre à 1 = probablement premier; 2 = surement premier
    $j = 0; $jMax = 100; // nombre des nombres premiers successifs désirés
    $iMax = 10000; // boucle maximale pour les obtenir
    for($i = 0; $i < $iMax; $i++){
      // calcul (3x-1)(3x-2)/2 et renvoie renvoie le nombre premier impair qui est ou bien (3x-1) ou bien (3x-2)
      $s = $this->produitPremier($x); // selon la parité de x
      $pB = gmp_prob_prime($s); // test de primalité de RABIN-MILLER
      if ($pB === $classe) // on peut s'en passer parce que l'on est sûr d'avoir que des nombres premiers
        $tab[$j++] = $s; // on enregistre le résultat dans un tableau
      $x = gmp_add($x, "1");
      if ($j === $jMax)  break;
    }
    $end_time = microtime(true); // Temps de fin de l'exécution
    $execution_time = $this->temps_execution($start_time, $end_time); // Calcul du temps d'exécution
    $res = [$execution_time, gmp_strval($x), $i, gmp_strval(gmp_sub($x, $i)), $j];
    $res [] = $tab; // mémoriser les résultats et les données d'analyse
    $json_data = json_encode($res); // Conversion du tableau een JSON
    $nom_fichiers = "suite_de_nombres_premiers_" . $bits ."_bits_classe_" . $classe ."_". date('Y-m-d_H-i-s') . ".json"; 
    $votre_repertoire_de_destination = "/wamp64/www/result/";
    $destination = $_SERVER['DOCUMENT_ROOT'] . $votre_repertoire_de_destination . $nom_fichiers; // construire le repertoire de dépôt
    $repertoire = dirname($destination); // Extraire le chemin du répertoire
    if (!file_exists($repertoire))  // Créer les répertoires récursivement s'ils n'existent pas déjà
      mkdir($repertoire, 0777, true);
    file_put_contents($destination, $json_data); // enregistrer le fichier
    return $tab; // pour visualiser à l'écran, dans un var_dump($tab) par exemple
  }

La fonction testProduitPremiers a besoin des trois fonctions suivantes pour produire les nombres premiers désirés. Notez que au-delà d'une certaine taille le paramètre de la fonction de test de primalité de Rabin-Miller est fixé à 1


  public function produitPremier($x) 
  {
    // Calcul des expressions A et B
    $A = gmp_sub(gmp_mul("3", $x), "2");
    $B = gmp_sub(gmp_mul("3", $x), "1");
    $s = (TRUE === $this->estPair($x)) ? gmp_strval($B) : gmp_strval($A); 
    return gmp_strval($s);
  }

  /***************** 
   * generateRandomNumber génère un nombre aléatoire de numBits
   * mais elle ne garantit pas qu'on aura obligatoirement numBits
   */ 
  private function generateRandomNumber(int $numBits): string
  {
      
      $numBytes = ceil($numBits / 8); // Calculer le nombre d'octets nécessaires pour le nombre de bits spécifié
      $randomBytes = openssl_random_pseudo_bytes($numBytes); // Générer des octets aléatoires
      $binaryNumber = ''; // Convertir les octets en un nombre binaire
      for ($i = 0; $i < $numBytes; $i++) {
          $binaryNumber .= str_pad(decbin(ord($randomBytes[$i])), 8, '0', STR_PAD_LEFT);
      }
      $randomNumber = substr($binaryNumber, 0, $numBits);// Extraire les bits nécessaires pour obtenir un nombre du nombre de bits spécifié
      return $randomNumber;
  }
  
  // renvoie un nombre décimal aléatoire de x bits environ 
  public function renvoieNombreDecimalAvecEnviron(int $bits)
  {
    boucle:
    do
    {
      $mot_binaire = $this->generateRandomNumber($bits);
      $decimal = gmp_init($mot_binaire, 2); 
      $lg = strlen($mot_binaire);
    }while($lg < $bits);
    if($lg < $bits) goto boucle;
    return($decimal);   
  }

Cette fonction permet de cibler directement les candidats premiers associés à une structure triangulaire, évitant ainsi une exploration séquentielle classique.

3. Couplage avec le test de primalité

Ce filtrage intelligent, combiné au test de Miller-Rabin, permet une détection rapide des nombres premiers parmi les entiers de forme 6k±1, de manière ordonnée et parallélisable.